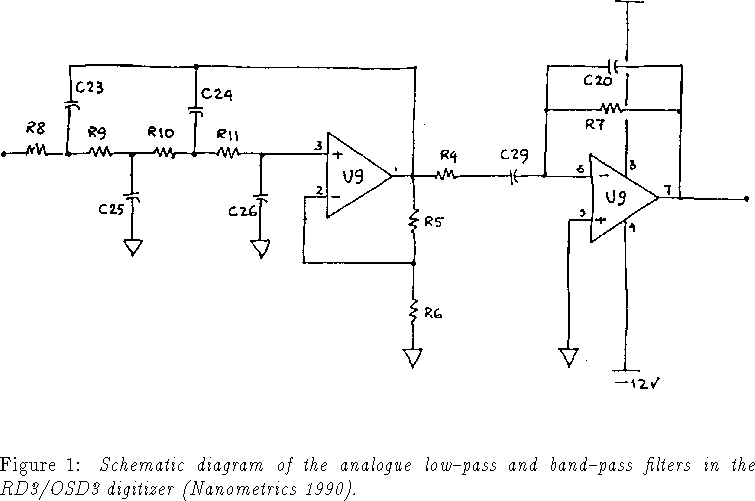
Referring to Figure 1 (Nanometrics 1990), the equations to be solved to find the relationship
between input and output signals ( 
and 
) of the fourth
order low-pass filter are:
After some algebra, equations 2-6 give:
where:
Inserting numbers for the components of the 4th order filter (see Appendix A) gives:
Similarly, for the second order bandpass filter, the frequency response is:
The frequency response of the two filters is then given by:
where:
and the k's are given by equation 12 and the b's by equation 13. Inserting numbers, the frequency response of the RD3 system is:
The function 
obviously has one zero at zero frequency.
The poles where found
using standard numerical routines (programmes zroots and laguer,
(Press et al. 1988))
and are:
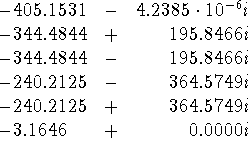
The frequency independent gain of the system is the multiple of the
pre-amplifier
(0.908), the post-amplifier ( 
)
and the filter gains ( 
V/bit), i.e.:
See Figure 4 in Nanometrics (1990) and Appendix B for explanations of the numbers given above. The frequency response of the RD3/OSD3 digitizer can then be written:
