Task 3: Methods for monitoring the local rock stress tensor

Start: July 1996 (month 5)
End: January 1998 (month 23)
Responsible partner: UUPP.DGEO
Cooperative partners: IMOR.DG

New methods and software have been developed to estimate a regional or local stress tensor based solely on microearthquake focal mechanisms and locations [53]. The inversion method is based on the work of Gephart and Forsyth [29] with significant changes in the treatment of focal mechanisms and in the criteria of choosing the correct fault plane from the two nodal planes. The inversion algorithm is implemented in the SIL system environment, takes full advantage of the SIL software for focal mechanisms [] and for absolute and relative location [] and is compatible with the visualization software.

We invert the focal mechanisms to obtain the directions of the three principal stresses and, $R =3D (\ensuremath{\sigma_{1}} - \ensuremath{\sigma_{2}} )/(\ensuremath{\sigma_{1}} - \ensuremath{\sigma_{3}} )$, a measure of the relative magnitude of the intermediate principal stress. We use a grid search over the lower hemisphere for the directions of the principal stresses and the size of R. For each stress tensor the direction of shear stress on the nodal planes are calculated and we minimize the angle, in the plane, between the observed slip direction and the theoretically calculated shear stress direction in the inversion. The misfit angle is used as the objective function to be minimized and can be weighted with the amplitude errors on the focal mechanisms, with dynamic source parameters such as the moment and can also be constrained to consider angles less than a certain value equal to that value to prevent overfitting the data. The misfit and confidence levels are calculated in a one-norm sense, following [29], and the confidence levels are further constrained using only non-redundant focal mechanisms [54].

To account for the uncertainties in the focal mechanisms we use the facilities provided by the SIL fault plane solution algorithm []. The algorithm provides a range of acceptable fault plane solutions for each event, in the same way as a 95% confidence level, where each fault plane solution has a specific amplitude error. The amplitude error is used as a weight in the misfit calculation. We include the whole range of mechanisms for each event and calculate the misfit of each focal mechanism, in the end choosing the mechanism which gives the lowest misfit. 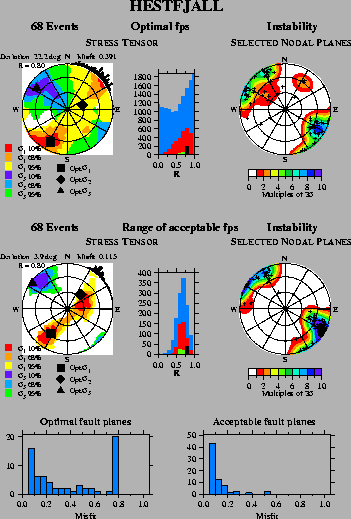This significantly improves the stress tensor inversion (Figure 6).

  

Figure: Results of stress tensor inversion of 68 microearthquake focal mechanisms in Hestfjall, Iceland. The upper two rows show lower hemisphere equal area projections, in the left column are the resulting principal stress directions with 10%, 68% and 95% confidence limits and the optimal solutions marked by a black square ($\sigma _1$), a black diamond ($\sigma _2$) and a black triangle ($\sigma _3$). Deviation is the average angle between observed slip and estimated shear stress and misfit is the weighted deviation, both for the optimal solution. R is the relative size of the intermediate principal stress. The black rose diagram around the circle is the 95% confidence limit for the direction of maximum horizontal compression. The middle column histogram shows the confidence regions for R and the right column shows the nodal planes that the inversion algorithm picked as fault planes. The plus signs are the poles to the individual planes. They are overlayed by a Kamb contour diagram. The upper row shows the result when only the optimal fault plane solutions (FPS) were included in the inversion and the middle row is the result when a range of acceptable FPS were used for each event. The third row shows histograms over the misfits of the individual FPS. Both inversions were performed with the instability plane selection criterion. The misfit is reduced significantly and the confidence limits shrunk markedly when using the range of acceptable FPS.

For each tested stress tensor all acceptable focal mechanisms are thus tested, the best fit mechanism is chosen for each event and all the chosen misfits added to a final misfit for that stress tensor.

The crucial point of choosing which nodal plane to include in the inversion, i.e. choosing the fault plane, has been tackled with three different methods (Figures 6 and 7):

  

Figure 7: Same 68 microearthquakes as in Figure 6 but now inverted with different nodal plane picking algorithms. Both examples in this figure have been inverted with acceptable fault plane solutions (FPS). In the upper row we have used the slip angle plane selection criterion to determine the fault planes. In the bottom row the plane with lowest stability, calculated using a simple Mohr-Coulomb failure criteria, was chosen as the fault plane. In addition six events have been located to a fault plane and thus constrained to only use FPS with the same direction as that plane. The slip angle inversion favours a normal faulting stress regime, although there are strike-slip regimes within the confidence levels. When inverting with predefined planes the stress tensors are more strongly polarized into a strike-slip and a normal faulting regime, both equally probable. The slip angle method selects very different fault planes from the instability inversions. We infer that the correct stress tensor can be distinguished only with knowledge of which planes slipped.

• Slip angle. The most common method today is to choose the nodal plane that shows the smallest misfit, i.e. the smallest angle between observed slip and estimated shear stress, in the tested stress field.
• Instability. We designed a new method of choosing the most unstable nodal plane in the current stress field. Using a simple Mohr-Coulomb failure criterion we define instability as $I =3D \tau - \mu\sigma_{n}$, shear stress minus the product of the coefficient of friction and the effective normal stress. We showed that the dependence on $\mu$, which is a potential problem, can be handled consistently without assuming a local coefficient of friction. The instability criterion is appealing from a physical view point but gives slightly higher misfits than the slip angle method.
• Pre-defined fault plane. Using the SIL algorithm for absolute and relative location [] we can sometimes, with very high accuracy, locate a cluster of events to a common fault plane. For the events in the cluster only fault plane solutions in agreement with this fault plane are used in the stress tensor inversion, i.e. we have a pre-defined fault plane. This criterion is used together with either the instability or slip angle criterion for the events without pre-defined plane.

We want to emphasize that these methods only choose the fault plane! They are not part of the objective function and do not add to the misfit. The objective function is calculated on the chosen nodal plane. The methods to choose a nodal plane have been tested with both synthetic data and geological fault slip data where the correct fault plane is known. The slip angle and instability methods generally return similar stress tensors but the chosen fault planes vary significantly. Our tests indicate that instability method chooses the correct fault plane more often than the slip angle method.

We have applied our stress tensor inversion scheme to data from Hestfjall in the SISZ. Figures 6 and 7 show different stages in the inversion of 68 microearthquakes, ranging in local magnitude from -0.36 to 1.38 with a median at 0.24 and in depth from 3.2 to 7.4 km with the median depth at 5.7 km. It is evident from Figure 6 that using a range of acceptable fault plane solutions significantly improves the fit and accuracy of the inversion. The overall misfit is reduced by more than a factor three, the 95% confidence level shrinks to show two distinct stress states, either strike-slip or normal faulting, and the direction of horizontal compression, the black histogram on the perimeter, is concentrated at . Also the range in Ris reduced. Both inversions choose mainly subvertical nodal planes striking NNE-ENE. At the bottom of Figure 6 we see the histograms of the individual misfits on the selected nodal planes and there is a marked change to lower misfits for the acceptable focal mechanism inversion. The lack of misfits between 0.0 and 0.05 is due to a lower bound on the misfit corresponding to between observed slip and estimated shear stress.

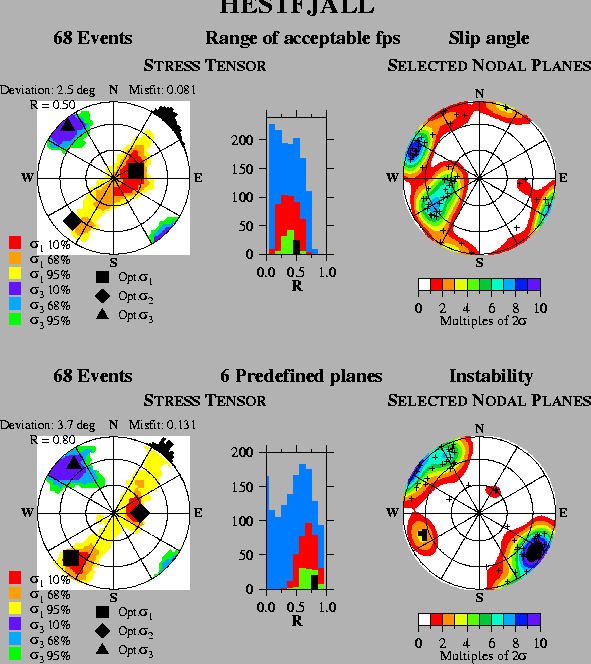
The results of using the three different criteria for choosing the fault plane can be seen in Figure 6, which shows the instability criterion inverse in the lower half, and in Figure 7, which shows the slip angle criterion on top and the pre-defined plane criterion, with instability for most of the events, below. All three inversions have been performed using the acceptable focal mechanisms. As expected the slip angle method gives the lowest misfit, since it has the largest freedom to choose well fitting planes. The pre-defined inversion has worse misfit than the instability inversion, also due to the lower degree of freedom when six of the events have fixed planes. All inversions yield approximately the same direction of maximum horizontal compression, , and all inversions have 95% confidence levels allowing both strike-slip and normal faulting regimes. The slip angle inversion, however, strongly favours normal faulting whereas the other two have almost equal misfits for the best fitting strike-slip and best fitting normal faulting stress tensors. The planes chosen by the different criteria vary markedly. The instability criterion choose mainly subvertical planes striking NNE-ENE, with some planes having lower dips, for the strike-slip stress state. The slip angle inversion choose both subvertical and subhorizontal planes with main strike directions of NNE and NW, which is similar to the planes the instability inversion choose for the normal faulting regime. Including pre-defined planes with the instability criterion yields even more subvertical planes but with an added group of NNW striking planes.

These 68 Hestfjall microearthquakes are thus compatible with both a strike-slip and a normal faulting state of stress. The strike-slip regime requires mainly NNE-ENE striking subvertical fault planes and the normal faulting regime requires some subhorizontal fault planes. Knowledge of the fault planes is thus necessary to distinguish between the two stress states. This can be gained either through a larger data set with more events with predefined planes or through extrapolation of surface fault mapping to the conditions at 5 km depth. We feel that the methods developed here have improved our chances of correctly identifying the state of stress in the crust through earthquake focal mechanisms.