 Introduction
Introduction  Movements on faults occur in earthquakes, aseismic slip or inelastic creep.
There are sequences of seismic quiescence followed by seismicity and so on.
Stresses are accumulated by plate motion and released in earthquakes and/or the
mentioned processes.
In the following, a model is described that accounts for plate motions and
earthquakes on Iceland.
Movements on faults occur in earthquakes, aseismic slip or inelastic creep.
There are sequences of seismic quiescence followed by seismicity and so on.
Stresses are accumulated by plate motion and released in earthquakes and/or the
mentioned processes.
In the following, a model is described that accounts for plate motions and
earthquakes on Iceland.
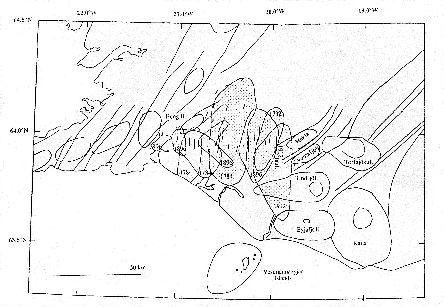
The SISZ is situated between two sections of the
Mid-Atlantic Ridge, the Reykjanes Ridge (RR) and the eastern volcanic zone
(EVZ). Even though the angle between the SISZ and the neighbouring ridges is
far from 90![]() ,
it is considered as a transform
fault (for the geological structures, see Figure 2).
Following the transform fault hypothesis, left-lateral shear stress is
expected along the E-W striking zone. This is equivalent to right-lateral shear
stress with N-S orientation. In fact, earthquakes seem to occur on N-S trending
faults ([,].
They are located side by side between the Hengill triple junction,
where the RR meets the low activity western volcanic zone (WVZ), and Hekla
volcano, a part of the EVZ [].
,
it is considered as a transform
fault (for the geological structures, see Figure 2).
Following the transform fault hypothesis, left-lateral shear stress is
expected along the E-W striking zone. This is equivalent to right-lateral shear
stress with N-S orientation. In fact, earthquakes seem to occur on N-S trending
faults ([,].
They are located side by side between the Hengill triple junction,
where the RR meets the low activity western volcanic zone (WVZ), and Hekla
volcano, a part of the EVZ [].
The questions to be solved are:
The method  The elasticity theory of dislocations is used to calculate the stress changes
induced by earthquakes with a double-couple strike-slip mechanism on an
extended rupture plane [61].
The elasticity theory of dislocations is used to calculate the stress changes
induced by earthquakes with a double-couple strike-slip mechanism on an
extended rupture plane [61].
The area investigated extends from 18 to 24![]() W and
from 63 to 65
W and
from 63 to 65![]() N. The origin of the coordinate system
is set to 24
N. The origin of the coordinate system
is set to 24![]() W, 64
W, 64![]() N
(Figure 36) it includes the SISZ, north and south of 64
N
(Figure 36) it includes the SISZ, north and south of 64![]() N,
N,
![\includegraphics[width=0.8\textwidth]{/heim/gg/pren1/final/roth/7B-1.eps}](img90.gif) |
The initial stress field is determined as follows: a tensional stress acting
N103![]() E (nearly parallel to the SISZ []
is assumed, due to ridge push or basal drag of the adjacent plates.
The stress magnitude, which is unknown, is set to a value that produces
left-lateral shear stresses in E-W direction as large as the stress drop
determined for the largest event (M=7.1) in the studied earthquake sequence.
Insofar, this stress is the minimum stress to be expected. The amount of this
minimum shear stress is 2.7 MPa (consistent with Gudmundsson [32],
who determined maximum values of 12 MPa from maximum displacement of superficial
fault traces found in the field). This shear stress corresponds to an
uniaxial tensional stress of -13.1 MPa. Tensional stresses at both ridges are
modelled as constantly being released to have zero values at the rifts. These
are the major disturbance of the unknown background stresses.
E (nearly parallel to the SISZ []
is assumed, due to ridge push or basal drag of the adjacent plates.
The stress magnitude, which is unknown, is set to a value that produces
left-lateral shear stresses in E-W direction as large as the stress drop
determined for the largest event (M=7.1) in the studied earthquake sequence.
Insofar, this stress is the minimum stress to be expected. The amount of this
minimum shear stress is 2.7 MPa (consistent with Gudmundsson [32],
who determined maximum values of 12 MPa from maximum displacement of superficial
fault traces found in the field). This shear stress corresponds to an
uniaxial tensional stress of -13.1 MPa. Tensional stresses at both ridges are
modelled as constantly being released to have zero values at the rifts. These
are the major disturbance of the unknown background stresses.
On this initial field, the stress changes due to earthquakes are iteratively superposed as well as the stress changes due to further spreading at the ridge segments based on an opening of 2 cm/year. This value is taken from []. The stress field before every event is thus the sum of the initial field, the stress drop of all preceding events, and the plate tectonic stress build-up since the starting time of the model, which is set to 1706, as discussed below.
Results were calculated for 56 x 44 test points covering 280 km in E-W direction and 220 km in N-S direction; i.e. the spacing is 5 km in both coordinates. Stresses were computed for a homogeneous half-space (as a starting model) with both Lamé's constants being 39 GPa. Although surface stress changes are calculated, these should be representative for crustal stresses using these values for the moduli, that are typical for oceanic crust [] and not for sedimentary layers at the surface.
Figures 37 and 38 give an example to illustrate the modelled effects: the
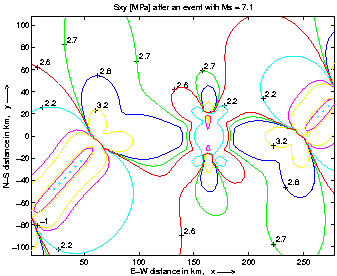 |
The earthquake data  All events in the SISZ with M
All events in the SISZ with M ![]() 6 since 1706 were used
(Table 2), following
[,,].
Even though the time of first 3 events is not exactly known, their occurrence
seems to be secured (in contrast to other events [])
and the catalogue is supposed to be complete from 1706 for earthquakes with
M
6 since 1706 were used
(Table 2), following
[,,].
Even though the time of first 3 events is not exactly known, their occurrence
seems to be secured (in contrast to other events [])
and the catalogue is supposed to be complete from 1706 for earthquakes with
M ![]() 6 [].
6 [].
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
The shape of their damage distribution and the strike of surface
breaks (Figure 39) further confirms strike-slip events on N-S trending
rupture planes [].
Nevertheless, all but one event are not recorded instrumentally.
The damage areas from historical records are not gathered by scientists and are
as usually biased by uneven population density. So the magnitudes and locations
are not very accurate.
 |
Determination of seismic moment, size of the fault plane, and average co-seismic slip from the magnitudes, was done as indicated in Table 2. As also discussed in [], there is the problem that fault lengths observed (e.g. 1912) are rather short compared to the magnitude of the events. Therefore a formula of Qian [60] was used here to calculate the rupture length. Additionally, the vertical fault width is limited by a brittle crustal thickness of about 15 km (cf. also the hypocenter vs. longitude plot of Stefánsson et al. [], their Figure 8) -- even though the effective short term crustal thickness reacting in brittle manner might be thicker for high frequency events as earthquakes compared to slow geological processes. For this first model, however, the co-seismic slip values were estimated to be lower (by a factor of 2) than from the global relation [] combined with the fault lengths used here. Hackman et al., had a reduction by a factor of 1.4 []. The reduction in slip values is equivalent to slightly reducing the magnitudes.
Earthquake fault planes near the Hengill triple junction were assumed to extend vertically to 7 km depth, for events further east 14 km were used (cf. the above mentioned hypocenter depth distribution). All ruptures were set to be oriented N-S.
The results  The stress fields at 18 dates were calculated: the pre- and post-seismic
situation for all 11 events and the stresses in 1998. The time before
5 events was too short to accumulate appreciable plate tectonic stresses since
the preceding event. In these cases, the post-seismic stress field of the
preceding event was set equal to the pre-seismic stress field of these
earthquakes.
The stress fields at 18 dates were calculated: the pre- and post-seismic
situation for all 11 events and the stresses in 1998. The time before
5 events was too short to accumulate appreciable plate tectonic stresses since
the preceding event. In these cases, the post-seismic stress field of the
preceding event was set equal to the pre-seismic stress field of these
earthquakes.
Figure 40 gives the initial stress field in 1706. The rift segments, lower
left and upper right, with about zero tensile stresses also show low shear
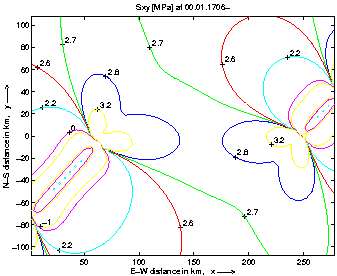 |
26 years later, at the break of the next large event, the stresses had slightly
increased, see e.g. between (160, 0) and (175, 0) in comparing Figures 41
and 42. The 1732, M=6.7 event then hit at (183, 0) in an area of high stress.
The two August 26 and 27, 1896, M=6.9 and M=6.7 events occurred at the same
position as the 1732, although the stresses at (178-183, 0) had not yet
recovered beyond the background value of 2.7 MPa, besides two very small areas
at (183,![]() 17). Figures 46, 47 and 48 show the pre- and
17). Figures 46, 47 and 48 show the pre- and
The stress field 16 years later, before the 1912 earthquake (M=7, at (187, -11))
had not changed much compared to 1896, but the stresses in the south part of
the epicentral area were rather high. Figure 49 shows the stress field after the
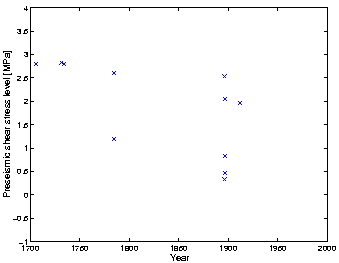
Figure 50 summarizes the mean shear stress level before each of the earthquakes
 |
Finally, the stress field was extrapolated to spring 1998, with the additional
stresses due to plate motion since 1912. Figures 51 and 52 show the shear
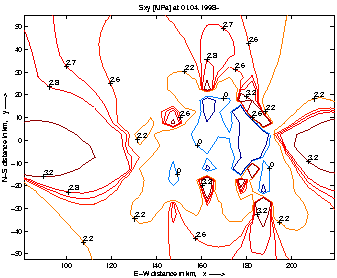 |
Discussion  The pre-seismic stress for most main shocks is high, 2.0-2.8 MPa. It is fairly
stable. As the initial stress field is unknown, the stress level at a site where
the earthquakes recur in the sequences provides a good test for the right
assumptions concerning the stress build-up due to plate movements: 1706
compared to September 6, 1896 and 1912; 1732 compared to August 1896. The tendency
with time towards slightly lower values, is an indication that the stress
increase due to rifting might have been assumed too low, i.e. the spreading
rate between 1706 and 1912 might be higher than 2 cm/year.
The pre-seismic stress for most main shocks is high, 2.0-2.8 MPa. It is fairly
stable. As the initial stress field is unknown, the stress level at a site where
the earthquakes recur in the sequences provides a good test for the right
assumptions concerning the stress build-up due to plate movements: 1706
compared to September 6, 1896 and 1912; 1732 compared to August 1896. The tendency
with time towards slightly lower values, is an indication that the stress
increase due to rifting might have been assumed too low, i.e. the spreading
rate between 1706 and 1912 might be higher than 2 cm/year.
Even though the earthquake rupture planes strike N-S, the stress changes calculated here affect the whole area of the SISZ. The areas west and east of the SISZ show constant stress increase in most parts. Here, the model should be improved to account for an extension of the spreading movements into these regions. Moreover, the initial stress field of 1706 could be reduced in the eastern part and the central part, where the first events did not occur before 1732 and 1734, respectively.
Smaller, instrumentally recorded events (as e.g. the above named Vatnafjöll event) will be included in a model with a denser test point distribution, based on the stress field determined here for 1912.
The known layering of the crust and upper mantle below Iceland is now introduced into the model, especially to account for inelastic layers, i.e. to include post-seismic relaxation processes. This will be compared to continuous GPS crustal deformation data as soon as these are available. A new code is prepared for this much faster, more accurate, and capable of including even more layers than the existing one.
Conclusions  The fact that almost all events occur in high stress areas indicates that this
first and simplified model can already explain the main features of the
behaviour of the SISZ. This is especially astonishing, when the fact is kept in
mind, that most (all but one) events used are not instrumentally recorded.
The fact that almost all events occur in high stress areas indicates that this
first and simplified model can already explain the main features of the
behaviour of the SISZ. This is especially astonishing, when the fact is kept in
mind, that most (all but one) events used are not instrumentally recorded.
The model goes beyond the standard earthquake moment release analysis as it includes the spatial location and extension of the events and provides an extrapolation to the present situation.