Model on the influence of volcanic loads

$\\$ The second modelling part tries to check end member models for the influence of volcanic loads, e.g. from Vatnajökull volcano, on the stress field in SISZ as produced by rifting. The calculations above are uninfluenced by such forces, i.e. the very large volcano (diameter 100 km) near the seismic zone (volcano centre to SISZ centre is about 160 km) is assumed to be totally in equilibrium due to isostasy and/or dynamic support by the up-welling magma in EVZ. Here, we supply a simulation of the load above sea level being not compensated (by buoyancy forces of a root or by other forces) and being compensated to 75%.

The method $\\$The method used here is the analysis of a load on a thin shell (lithosphere) above a substratum. As a first approach the substratum is assumed to be an elastic fluid. This will be changed to an inelastic solid material (asthenosphere) in later models. The work is based on [].

The thickness of the elastic plate is assumed to be 10 km, its Young's modulus is 71.4 GPa, its Poisson ratio is set to 0.25 (these parameters are chosen equal to those used by [], for a model for the northern EVZ). The density of the fluid is set to 3.1 kg/dm³. The volcano is approximated as having a radius of 50 km, an average height above sea level of 1.5 km, and a density of 2.8 kg/dm³ (in the fully uncompensated case) or 0.70 kg/dm³ (in the 75 % compensated case).

The results $\\$The stress field was calculated for the region which corresponds to the larger box in Figure 36, i.e. for Iceland and its surrounding area. The spacing of the test points is 20 km in both directions. This means that 30 x 36 points cover 600 x 720 km². Figure 36 also gives the ridge segments as entered into the model via calculations of the type of the former model for the SISZ. Only the region has been enlarged now. The SISZ is situated at (x = 200 km -- 280 km, y = -185 km) in this reference frame.

Figure 53 gives the orientations of the principal horizontal stress axes for

  

Figure: The orientations of the principal horizontal stress axes for the fully compensated model - without volcanic loads. The area covers the region of the larger box in Figure 36, i.e. Iceland and its surroundings, and includes the five ridge segments shown there. The scaling of the stress components is logarithmic, the sign is displayed by arrows (tension is shown by arrows in outward direction). The relative size of the components tend to look similar in this scaling, even if they differ by two orders of magnitude.

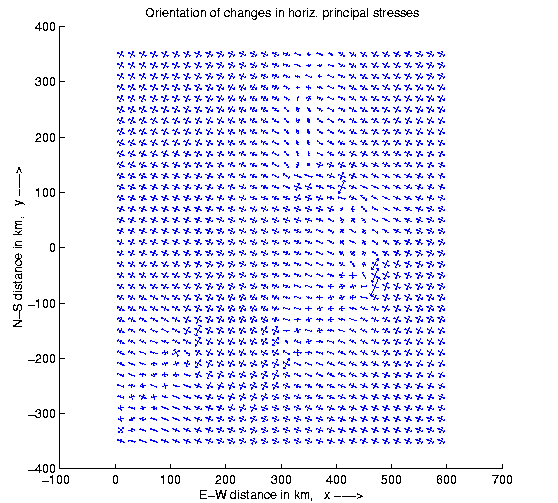the fully compensated model, i.e. the one uninfluenced by loads. As the emphasis is lead here on stress orientations, the scaling of the stress components is logarithmic. Therefore the sign (shown by arrow tips) is clearly visible at the cost of the relative size of the components being misleadingly similar. The SISZ shows a homogeneous stress field from east to west.

Figure 54 gives the orientations of the principal horizontal stress axes for

  

Figure: The orientations of the principal horizontal stress axes for the uncompensated model - with the full volcanic load. The area and the scaling are as in Figure 53.

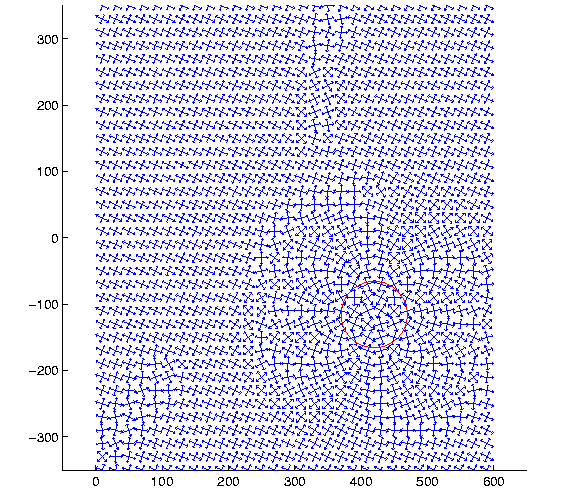the uncompensated model, i.e. the full visible load of Vatnajökull creates stresses below the volcano and the adjacent area. The stress orientations in the SISZ are disturbed, at least as far west as (220, -185).

Finally, Figure 55 gives the orientations of the principal horizontal stress

  

Figure: The orientations of the principal horizontal stress axes for the 75% compensated model - with 25% of the volcanic load. The area and the scaling are as in Figure 53.

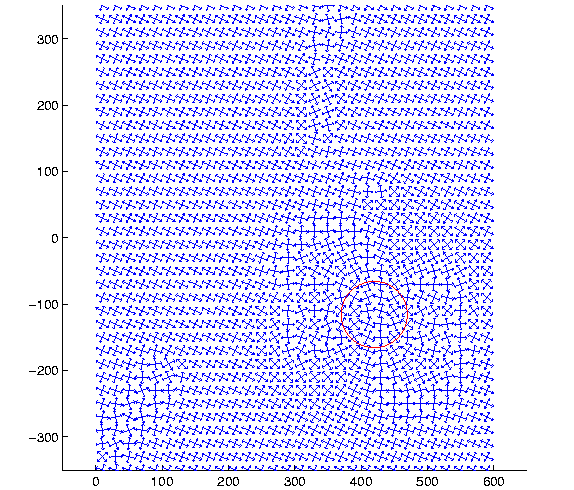axes for the 75% compensated model, i.e. only 25% of the visible load of Vatnajökull creates stress in addition to the ridge segments. Here, the stress orientations inside the SISZ are hardly influenced.

Preliminary conclusions $\\$We assume that the last model is more realistic than the fully uncompensated one. Thus the influence of the loading effect on stress orientation inside the SISZ seems to be small and may-be negligible.