As stated before, the Bernese processing software underestimates the true errors of the coordinate solutions because systematic errors or mismodelled parameters are not included in the formal error estimated by the processing software [Hugentobler et al. (2001)]. To obtain a resonable estimate of the daily coordinate errors we need to rescale the formal errors to obtain a realistic error estimation.
This problem has been dealt with in many studies, since all Bernese software users (and probably users of other software as well) necessarily need to face this important problem. However, there is no standard method approved by the GPS community and each study seems to use its own method to obtain a scaling factor to multiply the formal errors. Usually scaling factors are estimated by comparing the scatter of the data to the formal errors. The differences lie in how the scatter is defined and how the full covariance matrix is used to define the errors to be scaled.
The Bernese software offers a method to derive a scaling factor using the combination program ADDNEQ
[Hugentobler et al. (2001)],
[Braun (2000)].
This method estimates the rms repeatabilities
relative to a constant velocity model, meaning that the repeatabilitiy is
calculated after subtracting a best straight line fit (
![]() )
from the data.
From Figure 5 we see that a straight line
represents the data poorly. Offsets in the time series due to the
the June 2000 earthquakes and radome installation would bias the
repeatability estimation considerably.
Furthermore, if we remove
the coseismic displacement from the east component of VOGS
(described in more detail in Section 4.6) and subtract
a straight line, obtained by a least squares medhod (see Section 4.2.1), from
the data we obtain the residual1 of the time series:
)
from the data.
From Figure 5 we see that a straight line
represents the data poorly. Offsets in the time series due to the
the June 2000 earthquakes and radome installation would bias the
repeatability estimation considerably.
Furthermore, if we remove
the coseismic displacement from the east component of VOGS
(described in more detail in Section 4.6) and subtract
a straight line, obtained by a least squares medhod (see Section 4.2.1), from
the data we obtain the residual1 of the time series:
where ![]() is the vector of observed displacements, e.g. for the east component of VOGS
and
is the vector of observed displacements, e.g. for the east component of VOGS
and ![]() is the best line fit.
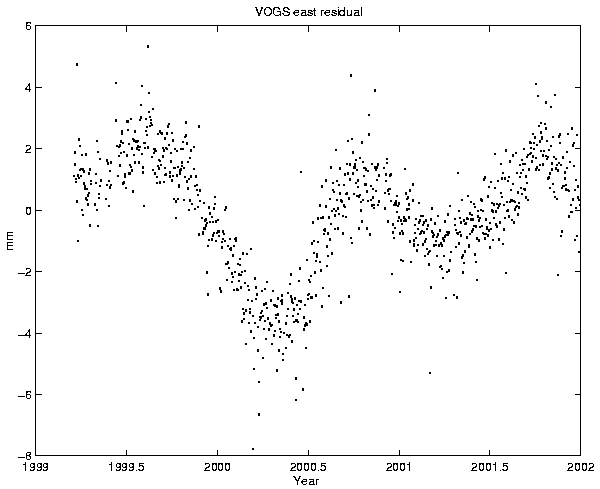
Figure 6 shows the residual of the east component
of VOGS relative to REYK. We see immediately from the figure that a straight
line model leaves a residual with periodic variations.
is the best line fit.
Figure 6 shows the residual of the east component
of VOGS relative to REYK. We see immediately from the figure that a straight
line model leaves a residual with periodic variations.
 |
[Árnadóttir et al. (2000)] use the Bernese network adjustment program COMPAR to calculate the average station coordinates for each week. COMPAR also returns the variation of the daily solutions from the weekly average. They compare the variances to the formal errors and obtain a scaling factor of 3 that they use for all coordinate components and sites. They also process the data using the GIPSY/OASIS software [Webb and Zumberge (1993)] and use there a scaling factor of 2.7 to rescale the coordinate and velocity errors.
[Lowry et al. (2001)] transform the covariance matrix, obtained using the Bernese software, to a local
east-north-up coordinate system and define the formal error as the corresponding
column sum of the covariance matrix. They estimate the repeatability scaling factors
using the 95th% ![]() repeatability of the coordinates, relative to a time varying
velocity model. This results in scaling factors (one for each coordinate direction
at each site) ranging from 2.0 to 3.9 (east), 1.6 to 3.6 (north) and 1.5 to 4.0 (up)
in their case.
repeatability of the coordinates, relative to a time varying
velocity model. This results in scaling factors (one for each coordinate direction
at each site) ranging from 2.0 to 3.9 (east), 1.6 to 3.6 (north) and 1.5 to 4.0 (up)
in their case.
In this study we define the formal errors as the square root of the diagonal elements of the covariance matrix and compare them to the weighted standard deviation, or repeatability, defined as
where N is number of data points, xi is the daily coordinate value, ![]() is the daily formal coordinate error and
is the daily formal coordinate error and ![]() the
mean coordinate value. Assuming
the
mean coordinate value. Assuming ![]() is a constant equal to
is a constant equal to ![]() ,
and
,
and
![]() is normally distributed with standard deviation
is normally distributed with standard deviation ![]() ,
then it is easy to use equation 2 to verify that
WSTD converges to
,
then it is easy to use equation 2 to verify that
WSTD converges to ![]() for large N.
for large N.
From Figure 6 we see there are clear annual variations in the data and we face the question whether the residual contains signal or if this is unmodelled noise. If the annual variations are assumed to be measurement noise then the standard deviation for the whole time series is an appropriate measure of the error. If the annual variations are considered a signal, be it from the earth or resulting from the processing, then the annual variations have to be removed from the time series before estimating the standard deviation. Here, the latter approach is chosen, and only the high frequency component is considered as measurement noise. This is in practice achieved by using only short segments (e.g. 50 days) of the time series to calculate WSTD.
We define the scaling factor as the ratio between the repeatability of the residual time series within a specific time interval, and the median formal error within the same time interval:
where j refers to the east north and up coordinate directions, t refers to the
time interval used, med refers to the median of the formal error ![]() and
WSTD is obtained from equation 2. The median of the formal errors
is chosen to represent the average error within a time interval because it is
a more robust estimator than the mean.
The coordinate errors obtained by using the scaling factor defined in
equation 3 do not represent the absolute positioning accuracy of the
daily solutions because they also rely on e.g. the coordinates of the reference station
(REYK). The rescaled errors, obtained using the scaling factor as in equation 3,
represent only the short-term repeatability of the daily solutions.
and
WSTD is obtained from equation 2. The median of the formal errors
is chosen to represent the average error within a time interval because it is
a more robust estimator than the mean.
The coordinate errors obtained by using the scaling factor defined in
equation 3 do not represent the absolute positioning accuracy of the
daily solutions because they also rely on e.g. the coordinates of the reference station
(REYK). The rescaled errors, obtained using the scaling factor as in equation 3,
represent only the short-term repeatability of the daily solutions.
Offsets in the time series due to the June 2000 SISZ earthquakes and equipment changes are removed (see Sections 4.1.1 and 4.6), as well as outliers (Section 3.2), before estimating the scaling factors. The time series for each station and each coordinate component are then split into kp segments including tdata points each where p refers to the station name as kp will depend on the length of the time series at station p. Each segment in each coordinate component is detrended using a weighted least squares method. From the detrended segments the WSTD and median formal errors are estimated to obtain scaling factors according to equation 3 for the east, north and vertical components for each segment. The mean of the kp scaling factors, for each component at each station, is calculated to obtain a single set of scaling factors in the east, north and vertical components for each station.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Despite the differences in the scaling factors between stations, we derive a single scaling factor for each coordinate component for the whole network. This is in order to simplify programming and discussion. It is not fair to simply take the average of the scale factors over all stations because a different amount of data lies behind each value. Thus we rather weigh the scale factors by the amount of data they are based on by taking the mean of all scaling factors obtained at each segment for all stations in each component. This results in scale factors of value 4.2 (east), 3.9 (north) and 2.3 (vertical), labelled "Composite" in Table 4. As final values we choose to use scale factors of 4.0 for the east and north components and 2.5 for the vertical component. The outlier detection has a significant effect on the scale factor values obtained. This will be discussed in more detail in the end of next chapter.
Equation 3 states that the median error and WSTD are
linearly related. A quick look at WSTD as a function of the median
error (Figure 7) shows
this is not a very good assumption.
However, we need to connect these two parameters and a linear relationship
seems no worse than any other.
![\begin{figure}
\centering
\mbox{\subfigure[]{\epsfig{figure=figures/scale_hypo...
... \subfigure[]{\epsfig{figure=figures/scale_hypoU.eps,width=5cm} }}
\end{figure}](img22.gif) |