Plates and plate velocities

The time series show motion due to the plate spreading across Iceland, seen as gradual increase in horizontal diplacements in the east-west and north-south components in Figures 8 to 20. From the time series we can calculate the velocities, i.e. average plate motions, of the sites by fitting a straight line to the data. However, care must be taken to remove instrumental errors such as offsets due to radome installation before estimating the velocities.

The proximity to the plate boundary and volcanoes and the displacements due to the SISZ 2000 earthquakes cause complications in the interpretation. The movements near active faults and plate boundaries are expected to be nonlinear and episodic [Heki et al. (1993)]. When stress is building up on the plate boundary prior to an earthquake the displacement rate across the plate boundary is lower than the average rate, if measured at close distance from the boundary. When an earthquake occurs a rapid change in position is observed near the causative fault of the earhquake. When stations are located far from the plate boundary the effects of the earthquake cycle are negligible because of the elastic properties of the crust and movements with constant velocities can be expected.

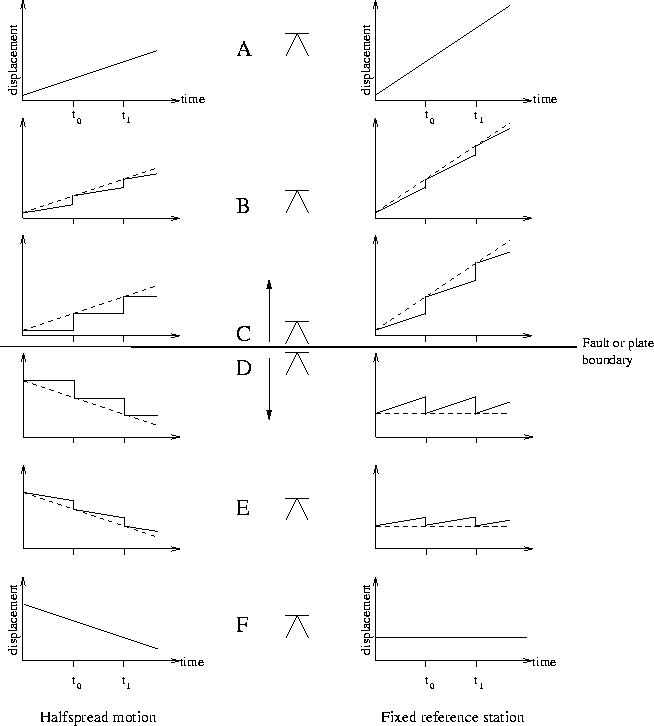
Figure 21 shows the anticipated displacements near a divergent plate boundary. The plates are assumed to be separating at constant velocities far from the plate boundary deformation zone. Near the fault zone the movements are episodic (occur at times t₀ and t₁ in Figure 21).

  

Figure 21: Anticipated motion of GPS stations (A to F) near a divergent plate boundary (or fault), assuming an elastic earth. The semi-triangles labelled A to F note permanent GPS sites. Stations A and F are very far from the plate boundary, C and D are very close to the plate boundary and stations B and E are at intermediate distances from the fault. The graphs to the left show the expected halfspread motion (normal to the fault) and the graphs on the right show the expected displacements relative to a fixed station (F), obtained by adding a velocity of half the full spreading rate to all stations. Time marks t₀ and t₁ note the times of major rifting episodes. (Adapted from [Heki et al. (1993)]).

This was for example observed in the Krafla rifting episode [Tryggvason (1984)]. At intermediate distances from the fault zone, the motion is a combination of constant velocities and episodic movement. The excact shape of the curves in Figure 21 and the distance to stations A to F from the fault zone depend on the rheology of the earth and the properties of the fault zone. Figure 21 is also valid for transform faults, or conservative plate boundaries, with displacements being parallel to the fault zone.

Because many of the ISGPS stations are located near the plate boundary it must be kept in mind what the observed velocities are physically representing. We must also keep in mind that the plate boundary in Iceland is not as simple as shown in Figure 21. If a station is sufficiently far from the plate boundary then the average velocity is representing the velocity of the rigid plates. If a station is near or within the fault zone, then over a period covering several earthquake cycles the average velocity is representing the velocity of the rigid plates. The time between major rifting episodes in the north has been estimated to be of the order of 100 to 150 years [Björnsson et al. (1979)] and the time period between large earthquake sequences in the SISZ ranges between 45 and 112 years [Einarsson et al. (1981)]. Thus we are only seeing a small part of the earthquake cycle in the time series.

The NUVEL-1A plate motion model [DeMets et al. (1994)] is computed from geological data, such as magnetic anomalies on the ocean floor, spanning millions of years. Recent plate velocities obtained using data from permanent GPS stations and other space-geodetic techniques are found to agree well with the NUVEL-1A model (e.g. [Sella et al. (2002)] and references therein). The NUVEL-1A model does not account for the witdh of plate boundaries, which is quite important for this study since most of the permanent GPS stations in Iceland are within or near plate boundaries.

In the following section the method to derive the site velocities and the associated uncertainties is described. With hindsight to Figure 21 we calculate velocities using three data sets: A) data including the coseismic displacements due to the June 2000 earthquakes (Section 4.2.2); B) data without the coseismic displacements (Section 4.2.3); and C) using only data spanning the period from August 31, 2000 to December 31, 2001 (Section 4.2.3).