The SISZ is a left-lateral E-W transform zone that
connects the Reykjanes peninsula (RP), and the
western volcanic zone (WVZ) to
the west to the eastern volcanic zone (EVZ) to the east
(Figure 1).
There have been sequences of several large earthquakes over a period of days to
years, starting with an earthquake in the eastern part of the SISZ
and continuing with events further to the west.
The time interval between large earthquake sequences in the SISZ
ranges between 45 and 112 years
[Einarsson et al.,1981].
Such series
of earthquakes occurred for example in
1630-1633, 1732-1734, 1784, 1896 and 2000.
Figure 2:
Map of the southwestern part of Iceland.
Thin black lines denote mapped
faults
( Einarsson and Eiríksson 1982; Einarsson and Sæmundsson 1987;
Erlendsson and Einarsson 1996).
The red dots show estimated epicenters of the MS=7.1 and
MS=6.7,
1784 earthquakes, that we use in our study, based on mapped surface faults
(P. Einarsson, personal communication, 1999).
The green dots show estimated epicenters of the two earthquakes
based on areas of destruction Stefansson/etal:1993.
The regions in which over half of the buildings were destroyed in the
earthquakes are shown with
N-S elliptical regions drawn in blue ( Björnsson 1978).
Corresponding intensity is MM VIII-IX ( Einarsson et al. 1981).
The black squares show current locations of towns and major villages.
|
Figure
2 shows
the estimated location of the epicenter for the earthquakes
based on areas of destruction (green dots) and surface faulting
(red dots). We use the locations shown with red dots in our study.
The epicentral location of the August 14 earthquake
does not greatly affect the velocity
calculations, since the map of peak velocities can be shifted
further west to match the location
shown with the green dot.
The outlined areas of destruction
correspond to Modified Mercalli intensity of VIII-IX
Einarsson/etal:1981.
Recently, a roughly 8 km long N-S surface rupture was mapped
in the epicentral area
of the M
S=7.1 event, using differential
GPS [
Jonsdottir et al., 1999.
Presumably the fault that ruptured in the earthquake was
considerably longer, but traces
at the surface are poorly preserved due to the surface geology
in the area.
In our study we calculate the velocities and stresses
generated by a large earthquake in the SISZ, taking the MS=7.1 earthquake
as an example.
In our simulations we are concerned with the large-scale effects
of a large earthquake in the SISZ, so we consider only simple
cases of a single planar rupture.
Based on observations of recent events, we assume that the
earthquake occurred on a N-S, right-lateral strike-slip fault,
at shallow depth.
We center our fault model on the
estimated epicentral location shown in Figure 2.
Since very little is known about the fault geometry,
hypocentral depth and location, we run several simulations varying
the fault geometry, rupture propagation, slip distribution
and
analyze the effects these parameters have on the peak ground velocity.
The goal is to identify which key parameters are important
in estimating reasonable ground velocities in
large earthquakes in the SISZ in the future.
We also calculate static coseismic stress changes
caused by the MS=7.1, August 14 earthquake
at the hypocenter of the MS=6.7, August 16
earthquake to examine the possible triggering of the later earthquake
by stress changes caused by the larger event.
The results from the Coulomb stress calculations are sensitive
to the fault locations we use in our study.
We use a staggered-grid velocity-stress finite-difference method described
by [
Olsen et al., 1995]
to solve the 3D elastic equations of motion [
Olsen, 1994].
The accuracy is fourth-order in space and second-order in
time. To limit reflections from the model boundaries we
apply absorbing boundary conditions to the sides
of the model [
Clayton and Engqust, 1977], and
add a zone of attenuative material
(25 nodes) on the sides and bottom of the model [
Cerjan et al., 1985].
The model parameters for the two grid spacings
are shown in Table 1.
Table 1:
Parameters for velocity simulations.
| Parameter |
250 m grid |
400 m grid |
| Spatial discretization (km) |
0.25 |
0.4 |
| Temporal discretization (s) |
0.015 |
0.024 |
| Number of E-W grid points |
481 |
320 |
| Number of N-S grid points |
319 |
219 |
| Number of vertical grid points |
115 |
97 |
| Number of time steps |
7000 |
5000 |
| Simulation time (s) |
105 |
120 |
| Maximum frequency resolved (Hz) |
1.5 |
1.0 |
|
The simulation is done for a volume of about 108  67 km
horizontally and 28 km vertically.
There is no anelastic attenuation in the earth model.
The surface velocities we are studying are
relatively insensitive to the value of Q [Graves, 1998].
We use the SIL P- and S-wave velocity model that is
used to locate earthquakes in Iceland, based on the refraction measurements of
Bjarnason et al. (1993b).
The SIL model is shown in
Figure 3.
67 km
horizontally and 28 km vertically.
There is no anelastic attenuation in the earth model.
The surface velocities we are studying are
relatively insensitive to the value of Q [Graves, 1998].
We use the SIL P- and S-wave velocity model that is
used to locate earthquakes in Iceland, based on the refraction measurements of
Bjarnason et al. (1993b).
The SIL model is shown in
Figure 3.
Figure 3:
The SIL velocity model and densities
for the southwestern part of Iceland.
The P- and S-wave velocities are shown in km/s, as a function of depth.
The density (rho) is shown with a dashed line,
on the same scale in units g/cm3.
|
The source is described by adding
-Mij(t)/V to Sij(t), where Mij is
the ij-component of the moment tensor, V=dx3 is the cell volume, and
Sij(t) is the ij-component of the stress tensor on the fault at time t.
The fault is discretized according to the grid spacing (i.e., 400 m and 250 m).
We use an isosceles triangular slip-rate function with an effective rise time
of 1.5 s at all the nodes of the fault.
The rupture is propagated radially out from the hypocenter at time
t=0 to the remaining grid points on the fault at a rate of
vr. We test both cases of constant rupture velocity (vr=2.7 km/s)
and variable rupture velocity (vr=0.85 vs).
The synthetic seismograms produced are low-pass filtered to 1.0 Hz with a 4-pole
Butterworth filter,
before calculating the peak velocities.
This corresponds to an accuracy of 5 points per minimum S-wave velocity.
Based on mapped surface faults and information from recent earthquakes in the
SISZ,
we simulate the M
S=7.1, 1784 earthquake as a bilateral,
purely right-lateral strike-slip rupture on a N-S oriented
vertical fault plane.
The fault parameters are listed in Table 2.
Table 2:
Fault model parameters. Parameters marked with 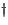 are
varied for different cases.
are
varied for different cases.
| Parameter |
Value |
| Longitude of center of fault |
20.37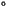 W W |
| Latitude of center of fault |
63.97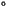 N N |
Hypocenter depth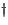 |
5, 10 km |
Fault length along strike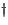 |
20, 50 km |
Fault width along dip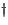 |
10, 15 km |
| Fault dip |
90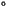 |
| Fault strike |
0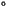 |
| Rake |
180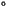 |
Moment (
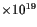 Nm)
Nm) |
5.37 |
Rupture velocity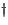 |
2.7 km/s, 0.85vs |
| Rise time |
1.5 s |
|
We vary some of the fault parameters (fault length and width,
hypocentral depth and location) as well as the
slip distribution, to evaluate
their effect on the surface velocities. We examine the end member
cases of a short fault (20 km long) and a long fault (50 km long).
It is likely that the earthquake ruptured a 30-40 km long fault.
The estimated thickness of the brittle crust in the
SISZ varies from about 5 km at the western end to about 12-15 km
at the eastern end [Stefansson et al., 1993,Tryggvason et al., 2000].
In our calculations we consider faults extending vertically down to
10 and 15 km.
There is no empirical formula relating the surface wave magnitude,
MS, and seismic moment, M0, in the SISZ.
A general formula is
log(M0)=1.5MS + 16.1, e.g., Lay and Wallace (1995),
which gives
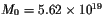 Nm.
An empirical formula derived for Iceland, relating the
local magnitude, ML, and the seismic moment, is given by
log(M0)=10.5+1.3ML
[Agustsson et al., 1999].
Using this relation we obtain a value of
Nm.
An empirical formula derived for Iceland, relating the
local magnitude, ML, and the seismic moment, is given by
log(M0)=10.5+1.3ML
[Agustsson et al., 1999].
Using this relation we obtain a value of
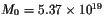 Nm, which we
use for the models in our simulations.
Nm, which we
use for the models in our simulations.
In the following sections we compare the calculated three-dimensional
peak velocities at the free surface
for several different models.
We start with the simplest case of uniform moment and
use that as our reference model and
explore the
effect of varying fault geometry and hypocenter location.
We then allow the rupture velocity to vary and compare cases
of variable fault depth to the reference case.
We examine the effect of
heterogeneous slip distribution on the fault, and
finally increase the maximum frequency to 1.5 Hz by decreasing the grid spacing.
The moment for each subfault (ij) is
Mij=
M0/
N, where
M0 is the total seismic moment and N is
the number of subfaults.
Mij is therefore constant for each subfault.
The slip on each subfault,
sij, is calculated from the moment
of each subfault, using the relation

.
The shear modulus is,

,
where
vs is
the S-wave velocity and

is density,
both of which increase with depth.
The slip is therefore not constant over the fault, but decreases with depth.
We refer to these models as uniform moment models, since the slip
is not uniform on the fault, although they
are often called uniform slip models in the literature.
If the earth model is a homogeneous half-space, uniform moment implies
uniform slip.
Our reference model is a
planar 50 km long, N-S oriented, vertical fault,
extending from the free surface down to 15 km depth.
The average motion on the fault is about 2.5 m of right-lateral strike-slip.
The hypocenter is at the center of the fault at 10 km depth.
The fault rupture propagates radially out from the hypocenter
with a constant rupture velocity of 2.7 km/s.
The rupture propagates from the
hypocenter to the ends of the fault in about 9 s.
Figure 4 shows a map view of the
calculated peak velocities at the free surface for this model.
Figure 4:
Peak velocity maps for the reference model with
400 m grid spacing.
The fault is 50 km long and extends from the surface down to 15 km depth.
The slip is uniform right-lateral strike-slip.
The hypocenter is in the center of the fault at 10 km depth.
The rupture propagates radially out from the hypocenter with a
constant rupture velocity of 2.7 km/s.
The N-S line shows the surface trace of the fault model.
The squares depict current locations of towns and major villages shown in Figure 2.
The N-S elongated area corresponding to MM VIII-IX is also shown.
The color scale extends from 0 m/s (dark blue) to 2.0 m/s (red).
The top panel shows the E-W component, the center panel shows
the N-S component, and the bottom panel shows the vertical component.
|
The top panel shows the E-W component, the center panel
shows the N-S component, and the bottom panel shows
the vertical component.
Figure 5:
Normalized peak velocities for the same
model as shown in Figure 4.
Each component of the peak velocity has been divided by the
maximum peak velocity for that component.
The color scale extends from 0 (dark blue) to 1.0 (red).
|
The maximum peak velocity
is 3.9 m/s in the E-W direction, 2.9 m/s
in N-S direction and 1.0 m/s in the vertical direction.
The color scale extends from 0 m/s (dark blue) to 2.0 m/s (red).
The squares show the locations of towns and major villages
in the area (see also
Figure
2).
The surface projection of the fault is shown with a straight
line along N-S. We also show the outlines of the area of destruction
in the M
S=7.1, 1784 earthquake. The largest N-S and vertical
peak velocities lie within that area. The maximum peak velocities
occur in the E-W direction, because of
rupture directivity effects in which the
amplitudes of the SH waves increase in the direction of
rupture propagation
(
e.g., Lay and Wallace 1995).
The patterns of the peak velocities are symmetric about the fault trace,
both along and perpendicular
to strike, for all the velocity components, as expected for a bilateral
rupture starting at the center of the fault.
The fault-parallel component (N-S) shows fairly large
peak velocities
out to several tens of kilometers away from the fault.
The coherency of long-period radiation is maximized in
uniform moment models, generating extremely large motions.
In order to compare our reference model with other models,
we normalize the surface peak velocities
by the maximum value for the corresponding component, i.e.,
3.9 m/s for E-W, 2.9 m/s
for N-S and 1.0 m/s for the vertical component, respectively.
Figure 5 shows the
normalized peak velocities for our reference model.
The color scale extends from 0 (dark blue) to 1.0 (red).
In subsequent plots the peak
velocities for the different models are normalized by the same
values.
Figure 6:
Normalized peak velocities
for a model with 400 m grid spacing and uniform moment. The
fault is 50 km long and extends from the surface down to 15 km depth.
The hypocenter is in the center of the fault at 5 km depth.
|
Figure
6
shows the same as Figure
5 for
the same model parameters, except the hypocentral depth is now 5 km
rather than 10 km.
Decreasing the hypocentral depth concentrates the large peak velocities
near the fault trace at the center of the fault,
for the fault-parallel
and vertical components, and
at the ends of the fault for the horizontal component.
The maximum value of the vertical and fault-parallel components of the
peak velocity decreases
slightly as the hypocentral depth decreases, whereas the maximum
value of the fault-perpendicular component increases.
Figure 7:
Normalized peak velocities for a model
with 400 m grid spacing and uniform moment. The
fault is 50 km long and extends from the surface down to 10 km depth.
The hypocenter is in the center of the fault at 5 km depth.
|
Figure
7 shows the same as
Figure
5 for
the same model parameters, except the down-dip fault width
is 10 km rather than 15 km.
The hypocenter is located at the center of the fault at 5 km depth.
A narrow fault increases the peak velocities significantly near the fault.
This is understandable because the moment and slip on each subfault increases,
when the fault area decreases.
The average slip for this model is about 4 m.
The overall effect of a narrow fault model is to increase all components
of the surface peak velocity near the fault.
Figure 8:
Normalized peak velocities
for a model with 400 m grid spacing and
uniform moment. The
fault is 20 km long and extends from the surface down to 15 km depth.
The hypocenter is in the center of the fault at 10 km depth.
|
Figure
8 shows the same as
Figure
5 for
the same model parameters, except the fault length
is 20 km rather than 50 km.
The average slip for this model is about 5 m.
A short fault produces higher peak velocities than a long fault,
because again the moment and slip on each subfault
increase when the fault area decreases.
The peak velocities of the fault-parallel component are also significantly
larger
away from the short fault. The maximum
value is in the fault-parallel direction, as opposed to
the fault perpendicular
direction found for the 50 km long fault.
This is due to the different aspect ratio for this fault model,
i.e., it is almost equal in length and width.
The other peak velocity components are less amplified.
Figure 9:
Normalized peak velocities
for a model with 400 m grid spacing and
uniform moment. The
fault is 20 km long and extends from the surface down to 10 km depth.
The hypocenter is in the center of the fault at 5 km depth.
|
Figure
9 shows the same as
Figure
8 for
the same model parameters, except the
fault extends down to 10 km rather than 15 km, and the hypocentral depth
is 5 km rather than 10 km.
Decreasing the fault area further increases the peak velocities,
as the slip and moment for each subfault
scale inversely with the size of the fault, when we assume a constant moment
for the whole fault.
The average slip for this model is about 10 m.
Comparing Figures
5 and
9
shows that for the same magnitude of the earthquake, decreasing the fault area
increases the peak velocities for all components.
As we decrease the area of the fault, we approach a point source, and
the N-S velocity component approaches a S-wave radiation pattern,
while the vertical component takes on a P-wave radiation pattern.
Figure 10:
Normalized peak velocities for a model with 400 m grid spacing and
uniform moment. The
fault is 50 km long and extends from the surface down to 15 km depth.
The hypocenter is near the southern end of the fault at 10 km depth.
|
Figure
10 shows the same as
Figure
5 for
the same model parameters, except the
hypocenter is now near the southern end of the fault.
The rupture is therefore almost unilateral.
The pattern of peak velocities is shifted towards the hypocenter
and broadens toward the north, particularly the horizontal components.
This model shows clearly the effect of rupture directivity
on the calculated velocities, which amplifies the fault-perpendicular component.
The rupture propagates from south to north, starting at the southern
end of the fault. In this case,
the peak velocities are lower to the south of the
epicenter and larger at the northern end,
compared to the scenario where the rupture starts in the center of the fault.
We examined the effect of vertically-varying crustal structure
by comparing our reference model to
a half space model with constant
vp and
vs velocities.
This model has a constant right-lateral strike-slip of
2.4 m. The fault is 50 km long
and extends from the surface down to 15 km depth.
Figure
11
shows the normalized peak velocities for the half space model.
Figure 11:
Normalized peak velocities for a half space
model with 400 m grid spacing and uniform moment. The
fault is 50 km long and extends from the surface down to 15 km depth.
The hypocenter is at the center of the fault at 10 km depth.
|
The model produces relatively small
surface peak velocities compared to those for the layered model.
This can be explained by the low
vp and
vs velocities
near the surface in the layered model effectively
trapping P- and S-waves.
We examined the effect of allowing the rupture velocity (
vr) to vary,
rather than keeping it fixed at 2.7 km/s.
Figure 12:
Normalized peak velocities for a model with
400 m grid spacing and uniform moment. The
fault is 50 km long and extends from the surface down to 15 km depth.
The hypocenter is in the center of the fault at 10 km depth.
The rupture velocity is
vr = 0.85 vs.
|
Figure
12 shows the same as
Figure
5, except the
rupture velocity is now
vr = 0.85
vs.
Note that the rupture velocity decreases as we approach
the surface, since it is
a fraction of the S-wave velocity.
Comparing Figures
12 and
5 we see that the maximum peak
velocities are smaller for the variable rupture velocity model
than for our reference model,
particularly the fault-perpendicular component.
This is caused by a decreased coherence of the rupture propagation.
We then examine a model with variable rupture velocity, where
the top of fault does not reach the surface, but is buried at 4 km depth,
and the fault extends down to 15 km.
As before, when decreasing the area of the fault, the slip and moment
of each subfault increases.
Figure 13:
Normalized peak velocities
for a model with 400 m grid spacing and
uniform moment. The
fault is 50 km long and extends from 4 km depth down to 15 km depth.
The hypocenter is in the center of the fault at 10 km depth.
The rupture velocity is
vr = 0.85 vs.
|
Figure
13 shows the normalized
surface peak velocities for this case.
A comparison of Figures
13 and
12 shows
that the peak velocities decrease significantly if the fault
does not reach the surface, particularly for the fault-parallel
and vertical
components of motion. The change in the
fault-perpendicular component is less significant.
A fault that reaches the surface produces higher
peak velocities at the surface than a buried fault.
The rupture velocity effects the peak velocities, but is less
critical than the depth of rupture.
As mentioned earlier, the constant slip models produce large
peak velocities in the near-source region if there are low-velocity
layers present.
If the fault does not rupture to the surface these shallow
low-velocity layers are less important.
We now examine how a heterogeneous slip distribution affects
the surface peak velocities.
We use a scaled version of the slip model estimated for the
1992 M=7.2 Landers earthquake [
Wald and Heaton, 1994],
on a 400 m grid. The slip on each subfault is scaled
such that the seismic moment of the entire fault is equal to
5.37
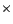
10
19 Nm. The moment is therefore
not constant on each subfault
as it is in the uniform moment models.
Figure
14 shows the slip distribution
model. The slip ranges from 0 m (dark blue) to 4.5 m (dark red).
Figure:14
Slip distribution along the fault
used to calculate peak velocities for 400 m grid
spacing. The
fault is 50 km long and extends from the surface down to 15 km depth.
The southern end of the fault is at 0 km.
The colors show the amount of slip from 0 m (dark blue)
to 4.5 m (dark red).
The magnitude of the slip in each patch is scaled such
that the total moment for the earthquake is 5.37 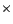 1019 Nm.
1019 Nm.
|
The fault is 50 km long, extending vertically from the surface
down to 15 km depth. The rupture starts at the center of
the fault at 10 km depth and propagates bilaterally from
the hypocenter, with a
constant velocity.
The calculated surface peak velocities for this model are shown in
Figure
15.
Figure 15:
Normalized peak velocities
for a model with 400 m grid spacing and
variable slip distribution. The
fault is 50 km long and extends from the surface down to 15 km depth.
The rupture starts at the center of the fault at 10 km depth.
The rupture velocity is 2.7 km/s.
|
In general, the largest peak velocities correspond to areas of large slip
in the model.
We see
that the peak velocities for the variable slip case are much smaller
compared to those for the uniform moment case for all components of motion
(Figure
5),
in particular the fault-parallel component.
The heterogeneous slip model has less moment on each subfault
at shallow depth than our reference model, which may account
for part of the difference.
The grid spacing is an important factor in these simulations, as
smaller grid spacing allows higher maximum frequencies
(
fm). A model with a 250 m grid spacing allows
simulation of
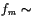
1.5 Hz, whereas a 400 m grid is limited to
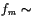
1.0 Hz,
for our velocity model, assuming at least 5 points per minimum wavelength.
Figure:16
Normalized peak velocities for uniform moment
case with 250 m grid spacing (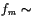 1.5 Hz). The
fault is 50 km long and extends from the surface down to 15 km depth.
The hypocenter is in the center of the fault at 10 km depth.
The peak velocities are normalized by dividing each component by the
maximum value for each component from the 400 m grid model
(Figure 5).
1.5 Hz). The
fault is 50 km long and extends from the surface down to 15 km depth.
The hypocenter is in the center of the fault at 10 km depth.
The peak velocities are normalized by dividing each component by the
maximum value for each component from the 400 m grid model
(Figure 5).
|
The computation time increases as 2
16 when the grid spacing is decreased by
a factor of 2 for a uniformly gridded model.
Figure 16
shows the normalized 1.5 Hz peak velocities for the reference model,
with finer grid spacing (250 m rather than 400 m).
The 1.5 Hz simulation increases the peak velocities by up to
a factor of 1.5 while the overall pattern
seen in Figures 16 and 5
is similar,
i.e., the maximum peak velocities are in the fault-perpendicular (E-W)
direction.
Figure
17
shows snapshots of the velocity field for the reference
model at times t = 4.8, 9.6, 12.0,
18.0, and 24.0 s.
Figure 17:
Snapshots of the velocities at times t = 4.8, 9.6, 12.0,
18.0, and 24.0 s in map view for the reference model shown in
Figure 4.
Red is positive and blue is negative velocity.
Vx is fault-perpendicular, Vy is fault-parallel and Vz is
vertical velocity.
The P-wave amplitudes are so small that they are not seen
in the figure. The S-waves can be detected, but the largest amplitudes
at times after t=12 s are the Love-waves.
The S-waves arrive in Reykjavík between 18 and 24 s.
Reflections from the boundaries of the model occur after t=18 s,
but these have lower amplitudes that the peak velocities
shown in previous figures.
|
The left panels show the fault-perpendicular component (E-W),
the center panels show the fault-parallel component (N-S), and
the panels on the right show the vertical component.
Red is positive and blue is negative velocity.
The rupture has propagated to the ends of the fault at time t
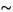
9 s
and the S-waves have reached Reykjavík at 24 s.
We clearly see the propagation of S- and Love-waves
in the plots for the fault-parallel component. The S-waves
are the first band of yellow color propagating west, out from the fault,
followed by larger amplitude Love-waves.
Figure
18
shows low-pass filtered synthetic seismograms for
the village of Hella, town of Hveragerði, and
the capital of Iceland, Reykjavík,
for the variable slip model shown in Figure
14.
Figure 18:
Synthetic seismograms for Hella, Hveragerði, and
Reykjavík calculated for the variable slip model
shown in Figure 14.
Vx, Vy, and Vzare velocities in E-W, N-S, and vertical direction, respectively.
The large amplitudes at Hveragerði and Reykjavík are Love-waves.
The small bumps in the Vx component at Hella after 12 s are
reflections from the southern boundary.
|
Hella is near the southern end of
the fault, Hveragerði is about 40 km to the west
and Reykjavík is about 70 km northwest of the fault center.
Their locations are shown in Figure
2.
We plot the velocities, v, where the subscripts
x, y and z, are E-W, N-S and
vertical direction, respectively, as a function of time.
The velocities are in m/s and time is in seconds.
The highest surface velocities are
observed at Hella which is in the near field. The maximum
velocity at Hella is in the fault-perpendicular
direction (E-W).
The maximum surface velocities at Hveragerði and Reykjavík are
in the fault-parallel direction (N-S).
Note that the velocity scale in Figure
18
for Hella is larger than
the scale for Hveragerði and Reykjavík.
The M
S=7.1 August 14, 1784 earthquake was followed two days later
by a M
S=6.7 earthquake about 30 km to the west of the August 14
epicenter (see Figure
2).
In this section we calculate
the static coseismic change in Coulomb failure stress caused by the first
earthquake to determine whether it is likely to have
triggered the second one.
We use the same fault parameters as in our reference model,
i.e.,
a vertical, right-lateral strike-slip fault, extending from the surface
down to 15 km depth. The fault is embedded in an elastic half-space.
We assume a constant slip over the fault
and a seismic moment of 5.37
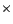
10
19 Nm. We compare
two cases of a 50 km long fault (the slip is then 2.4 m)
and a 20 km long fault (with 6.0 m of slip).
We assume that both earthquakes were
right-lateral strike-slip events on N-S oriented, vertical faults,
and that the hypocenter of the second event
was at 5 km depth.
We calculate the change in Coulomb failure stress (
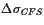 )
[Harris, 1998 ,Stein, 1999], using
)
[Harris, 1998 ,Stein, 1999], using
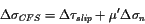 |
(1) |
where
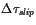
is the change in shear stress resolved in the
slip direction of the second earthquake
(
i.e., for these two earthquakes
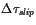
=
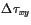
),
and
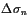
is the change in normal stress due to the first
earthquake, perpendicular to the second fault plane (here
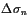
= -
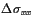
). Positive
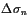
implies increased tension, hence the negative sign of
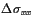
.
The ``apparent coefficient of friction'',
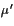
,
ranges typically from 0 to 0.6 [
Harris, 1998].
We use a value of
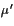
=0.4,
i.e., corresponding to a medium strength fault [
King et al., 1994].
A positive
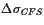
implies an increase in Coulomb
failure stress, indicating that the
first earthquake brought the second fault closer to failure.
It has been suggested that changes in CFS on the order of 0.1 bar
affect locations of aftershocks [
Harris, 1998].
We have not included the effects of a local stress field
in our calculations.
Figure 19:
Coseismic Coulomb stress changes at 5 km depth
for a 50 km long uniform slip model, in bars.
The black star shows the epicenter location of the MS=6.7, August 16, 1784
earthquake. The coastline and the location of the fault model
are shown with white lines.
|
Figure
19 shows the
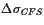
for a 50 km
long fault model
and Figure
20 shows the same for a 20 km long fault.
Figure 20:
Coseismic Coulomb stress changes at 5 km depth
for a 20 km long uniform slip model, in bars.
The black star shows the epicenter location of the MS=6.7, August 16, 1784
earthquake.
The coastline and the location of the fault model
are shown with white lines.
|
For the case of a 50 km long fault, we estimate a
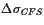
of -0.68 bars
at the assumed hypocenter location of the M
S=6.7 event (shown with a
black star in the figures).
A negative sign of
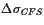
implies that a right-lateral fault is
less likely to break
at this location following the M
S=7.1 event.
In the case of a 20 km long fault the
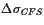
is 4.2 bars
at the hypocenter location of the second shock.
This is a very large change in CFS and more than ample to trigger the second
earthquake.
Based on our assumptions for the fault locations, it is
therefore more likely that a 20 km long fault
could have brought the second fault closer to failure
than a 50 km long fault, even with less slip on the short fault
than we assume.
These results are sensitive
to the fault locations we use in our study.
If the August 14 earthquake occurred further west, and the August
16 event further south, than we assume in our model, we can not rule out
the possibility of a 50 km long fault triggering the second event.
The pattern of
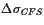 close to the fault
depends on the slip distribution, but at a distance of 30 km away from
the fault the values are similar to what is predicted by uniform slip models
with the same moment.
Our models do not include viscoelastic rheology, needed to explain the time
delay of three days between the earthquakes.
close to the fault
depends on the slip distribution, but at a distance of 30 km away from
the fault the values are similar to what is predicted by uniform slip models
with the same moment.
Our models do not include viscoelastic rheology, needed to explain the time
delay of three days between the earthquakes.
Our study indicates that
the predicted surface peak velocities vary considerably
between a fault that extends to the surface and a buried fault.
The depth to the top of the fault is therefore an important
variable in determining accurately the peak surface velocities.
Waves generated at shallow depth where the P-wave velocity
increases significantly with depth,
are trapped near the surface and generate
high surface velocities.
In our models this applies down to a depth of 6 km.
The mapped surface fractures in the SISZ suggest that the
large historical earthquakes ruptured to shallow depths, although
they may not have reached the surface along the entire trace of the fault.
The slip distribution is also important, particularly the
amount of slip at shallow depth.
The heterogeneous slip distribution model
produces a very different pattern and lower values
of peak velocities compared to our reference model.
This is probably because the heterogeneous slip model has
variable slip at shallow depth.
In a large earthquake, such as the M
S=7.1, 1784 event, we expect the
slip to have been strongly heterogeneous. Uniform moment
models will overpredict the peak velocities that we can expect in
a large earthquake in the SISZ.
These results are in agreement with a study by Graves (1998)
based on 3D finite difference simulation of a M=7.5 earthquake
on the San Andreas fault. He concludes that
``... accurate simulation of long period ground motions requires a realistic
source parametrization, including appropriate choices of
seismic moment and rise time, as well as the use of spatial and
temporal variations in slip distribution.''
In our study we have not examined the effect of changing the seismic
moment and rise time. Our simulations with large faults versus small
faults demonstrate the effect of changing the slip magnitude,
which clearly affects the calculated peak velocities.
We also find increased peak velocities with a higher maximum frequency.
The high frequency waves generated in this model would, however, be attenuated
if we included anelastic attenuation in our earth model, hence
decreasing the peak velocities.
Near the fault, most of the models predict that
the maximum velocity occurs in the fault-perpendicular
direction, due to the directivity effect.
Farther away from the fault, the
fault-parallel component (N-S) is larger than the other components.
The largest velocities expected in Reykjavík
are therefore found on the fault-parallel component
for a N-S oriented, vertical, right-lateral slip fault model.
We assume a one dimensional velocity structure for the whole area.
Our models would underestimate the peak velocities,
if basin structures are pronounced in South Iceland.
We calculated the Coulomb stress change for two end member cases,
i.e., a short (20 km) fault and a long (50 km) fault.
The calculations suggest that if
the MS=7.1, August 14, 1784 earthquake
ruptured a short fault it is more likely
to promote failure at the MS=6.7, August 16, 1784
hypocenter, than a 50 km long fault.
This result, however, depends on the relative locations of the
faults. The pattern of coseismic Coulomb stress change
shows that the first earthquake is likely to have triggered
the second earthquake if the southern end of the rupture
was due east of the epicenter of the second event.
A short fault rupture for the August 14 earthquake
agrees with the observations
that large historical earthquakes in Iceland generally occur on
short faults with anomalously
high stress drop [Bjarnason et al., 1993].
We are grateful to
Páll Einarsson,
Páll Halldórsson, Ragnar Stefánsson,
Sveinbjörn Björnsson,
Ingi Þ. Bjarnason, Kristín Jónsdóttir, and
Sigurður Th. Rögnvaldsson, who helped us determine the range
of reasonable parameters for the simulation and provided other necessary
background information on the 1784 earthquakes.
Critical review and comments from Kristín S. Vogfjörð and
Ingi Þ. Bjarnason greatly improved
this report.
The figures in this report were generated using the public domain
GMT software [
Wessel and Smith, 1991].
The velocity simulations in this study were performed on the SGI Origin 2000 at
the Material Research Laboratory, University of California at Santa Barbara.
Financial support for this project was provided in part
by the EC project PRENLAB-2 (contract number ENV4-CT97-0536) and
the Icelandic Research Council (RANNÍS), grants 981050098 and 981050099
(Þóra Árnadóttir).
- natexlab
- Ágústsson et al.(1999)Ágústsson, Linde,
Stefánsson and Sacks
-
Ágústsson, K., A.T. Linde, R. Stefánsson and S. Sacks 1999.
Strain changes for the 1987 Vatnafjöll earthquake in South
Iceland and possible magmatic triggering.
J. Geophys. Res. 104, 1151-1161.
- Árnadóttir et al.(1999)Árnadóttir,
Rögnvaldsson, Ágústsson, Stefánsson, Hreinsdóttir, Vogfjörð and
Þorbergsson
-
Árnadóttir, Þ., S.Th. Rögnvaldsson, K. Ágústsson, R. Stefánsson
,
S. Hreinsdóttir, K.S. Vogfjörð and G. Þorbergsson 1999.
Seismic swarms and surface deformation in the Hengill area, SW
Iceland.
Seismol. Res. Lett. 70, 269.
- Árnadóttir et al.(2000)Árnadóttir,
Geirsson, Bergsson and Völksen
-
Árnadóttir, Þ., H. Geirsson, B.H. Bergsson and C. Völksen 2000.
The Icelandic continuous GPS network - ISGPS, March 18,
1999 - February 20, 2000.
Rit Veðurstofu Íslands VÍ-R00002-JA02.
Research report, Icelandic Meteorological Office, Reykjavík, 36pp.
- Bjarnason and Einarsson(1991)
-
Bjarnason, I.Þ., and P. Einarsson 1991.
Source mechanism of the 1987 Vatnafjöll earthquake in South
Iceland.
J. Geophys. Res. 96, 4313-4324.
- Bjarnason et al.(1993a)Bjarnason, Cowie, Anders, Seeber and
Scholz
-
Bjarnason, I.Þ., P. Cowie, M.H. Anders, L. Seeber and C.H. Scholz 1993a.
The 1912 Iceland earthquake rupture: growth and development of a
nascent transform system.
Bull. Seism. Soc. Am. 83, 416-435.
- Bjarnason et al.(1993b)Bjarnason, Menke, Ólafur
G. Flóvenz and Caress
-
Bjarnason, I.Þ., W. Menke, Ó.G. Flóvenz and D. Caress 1993b.
Tomographic image of the mid-Atlantic plate boundary in
southwestern Iceland.
J. Geophys. Res. 98, 6607-6622.
- Björnsson(1978)
-
Björnsson, S. 1978.
Large earthquakes in South Iceland
(Jarðskjálftar á Suðurlandi).
Report and maps of a working group to the Civil Defense of
Iceland
(in Icelandic), 54pp.
- Cerjan et al.(1985)Cerjan, Kosloff, Kosloff and
Reshef
-
Cerjan, C., D. Kosloff, R. Kosloff and M. Reshef 1985.
A nonreflecting boundary condition for discrete acoustic and elastic
wave equations.
Geophysics 50, 705-708.
- Clayton and Engquist(1977)
-
Clayton, R. and B. Engquist 1977.
Absorbing boundary conditions for acoustic and elastic wave
equations.
Bull. Seism. Soc. Am. 71, 1529-1540.
- Einarsson et al.(1981)Einarsson, Björnsson, Foulger,
Stefánsson and Skaftadóttir
-
Einarsson, P., S. Björnsson, G. Foulger, R. Stefánsson and
Þ. Skaftadóttir 1981.
Seismicity pattern in the South Iceland seismic zone.
In:
D.W. Simpson and P.G. Richards (editors),
Earthquake prediction - an international review.
Maurice Ewing Series 4,
Am. Geophys. Union, Washington D.C., 141-151.
- Einarsson and Eiríksson(1982)
-
Einarsson, P. and J. Eiríksson 1982.
Earthquake fractures in the districts Land and Rangárvellir
in the South Iceland seismic zone.
Jökull 32, 113-120.
- Einarsson and Sæmundsson(1987)
-
Einarsson, P. and K. Sæmundsson 1987.
Earthquake epicenters 1982-1985 and volcanic systems in Iceland.
In: Þ.I. Sigfússon (editor),
Í hlutarins eðli. Map accompanying festschrift for
Þorbjörn Sigurgeirsson.
Menningarsjóður, Reykjavík.
- Erlendsson and Einarsson(1996)
-
Erlendsson, P. and P. Einarsson 1996.
The Hvalhnúkur fault, a strike-slip fault mapped within the
Reykjanes peninsula oblique rift, Iceland.
In: B. Þorkelsson (editor).
Seismology in Europe.
Papers presented at the XXV ESC General Assembly,
Reykjavík, Iceland, September 9-14, 1996,
498-505.
- Graves(1998)
-
Graves, R.W. 1998.
Three-dimensional finite-difference modeling of the San Andreas
fault: Source parametrization and ground motion levels.
Bull. Seism. Soc. Am. 88, 881-897.
- Halldórsson et al.(1984)Halldórsson, Stefánsson, Einarsson and
Björnsson
-
Halldórsson, P., R. Stefánsson, P. Einarsson and S. Björnsson 1984.
Earthquake risk: Dysnes, Geldinganes, Helguvík,
Vatnsleysuvík, Vogastapi and Þorlákshöfn
(Mat á jarðskjálfta- hættu: Dysnes, Geldinganes, Helguvík,
Vatnsleysuvík, Vogastapi og Þorlákshöfn).
Technical report
for the commitee for selecting locations for industrial sites.
Icelandic Meteorological Office and Science Institute, University
of Iceland (in Icelandic), 34pp.
- Harris(1998)
-
Harris, R. 1998.
Introduction to special section: Stress triggers, stress shadows, and
implications for seismic hazard.
J. Geophys. Res. 103, 24347-24358.
- Hreinsdóttir et al.(2000)Hreinsdóttir, Einarsson and
Sigmundsson
-
Hreinsdóttir, S., P. Einarsson and F. Sigmundsson 2000.
Crustal deformation at the oblique spreading Reykjanes peninsula,
SW Iceland: GPS measurements from 1993 to 1998.
J. Geophys. Res., submitted.
- Jónsdóttir et al.(1999)Jónsdóttir, Einarsson and
Hjörleifsdóttir
-
Jónsdóttir, K., P. Einarsson and V. Hjörleifsdóttir 1999.
Surface ruptures of the 1630 and 1784 South Iceland earthquakes
(Sprungukerfi Suðurlandsskjálftanna 1630 og 1784).
Geoscience Society of Iceland, Spring meeting
(in Icelandic).
- King et al.(1994)King, Stein and Lin
-
King, G., R. Stein and J. Lin 1994.
Static stress changes and the triggering of earthquakes.
Bull. Seism. Soc. Am. 84, 935-953.
- Lay and Wallace(1995)
-
Lay, T. and T.C. Wallace 1995.
Modern global seismology.
Academic Press, San Diego, 521pp.
- Olsen(1994)
-
Olsen, K.B. 1994.
Simulation of three dimensional wave propagation in the Salt
Lake Basin.
Ph.D. thesis, University of Utah, Salt Lake City, Utah, 157pp.
- Olsen et al.(1995)Olsen, Pechmann and Schuster
-
Olsen, K.B., J.C. Pechmann and G.T. Schuster 1995.
Simulation of 3D elastic wave propagation in the Salt Lake basin.
Bull. Seism. Soc. Am. 85, 1688-1710.
- Rögnvaldsson et al.(1998) Rögnvaldsson, Árnadóttir,
Ágústsson, Skaftadóttir, Guðmundsson, Björnsson, Vogfjörð, Stefánsson,
Böðvarsson, Slunga, Jakobsdóttir, Þorbjarnardóttir, Erlendsson, Bergsson,
Ragnarsson, Halldórsson, Þorkelsson and
Ásgeirsdóttir
-
Rögnvaldsson, S.Th., Þ. Árnadóttir, K. Ágústsson, Þ. Skaftadóttir, G.B. Guðmundsson,
G. Björnsson, K.S. Vogfjörð, R. Stefánsson, R. Böðvarsson, R. Slunga,
S.S. Jakobs- dóttir, B. Þorbjarnardóttir, P. Erlendsson, B.H. Bergsson,
S. Ragnarsson, P. Halldórsson, B. Þorkelsson and M. Ásgeirsdóttir
1998.
An earthquake swarm in Ölfus in November 1998
(Skjálftahrina í
Ölfusi í nóvember 1998).
Greinargerð Veðurstofu Íslands VÍ-G98046-JA09. Report,
Icelandic Meteorological Office, Reykjavík
(in Icelandic), 19pp.
- Stefánsson et al.(1993)Stefánsson, Böðvarsson, Slunga, Einarsson,
Jakobsdóttir, Bungum, Gregersen, Havskov, Hjelme and
Korhonen
-
Stefánsson, R., R. Böðvarsson, R. Slunga, P. Einarsson, S.S. Jakobsdóttir,
H. Bungum, S. Gregersen, J. Havskov, J. Hjelme and H. Korhonen 1993.
Earthquake prediction research in the South Iceland seismic
zone and the SIL project.
Bull. Seism. Soc. Am. 83, 696-716.
- Stein(1999)
-
Stein, R. 1999.
The role of stress transfer in earthquake occurrence.
Nature 402, 605-609.
- Thoroddsen(1899 and 1905)
-
Thoroddsen, Þ. 1899 and 1905.
Earthquakes in Iceland (Landskjálftar á Íslandi).
Hið íslenska bók- menntafélag, Copenhagen
(in Icelandic), 269pp.
- Tryggvason et al.(2000)Tryggvason, Rögnvaldsson and
Flóvenz
-
Tryggvason, A., S.Th. Rögnvaldsson and Ó.G. Flóvenz
2000.
Three-dimensional imaging of the P- and S-wave velocity structure
and earthquake locations beneath Southwest Iceland.
J. Geophys. Res., in press.
- Wald and Heaton(1994)
-
Wald, D.J. and T.H. Heaton 1994.
Spatial and temporal distribution of slip for the 1992 Landers,
California earthquake.
Bull. Seism. Soc. Am. 84, 668-691.
- Wessel and Smith(1991)
-
Wessel, P. and W.H.F. Smith 1991.
Free software helps map and display data.
EOS, Trans. Am. Geophys. Un. 72, 441 and 445-446.
Simulation of surface velocities and stress changes for
the MS=7.1, 1784 earthquake, Iceland
This document was generated using the
LaTeX2HTML translator Version 98.1p1 release (March 2nd, 1998)
Copyright © 1993, 1994, 1995, 1996, 1997,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 1784_rep.
The translation was initiated by Thora Arnadottir on 2000-09-28


 Thora Arnadottir
Thora Arnadottir
2000-09-28